How I Use Fibonacci Analysis To Make Money In The Market

First of all, let's discuss the "stigma" that surrounds Fibonacci analysis. The fundamental and academic community tends to despise anything and anyone that refers to Fibonacci. This is plain ignorance. Think about the academic community that actually believes in "Random Walk". It's 2016 and they are still pushing that nonsense. They're only making themselves sound stupid, so it's fine with me. But imagine trying to convince an old tenured professor, who is only used to people telling him how great he is, that Fibonacci analysis disproves his theories. Good luck with that....

With regards to the fundamental community, it's not even worth it. I've had multiple conversations with some of these people where they have literally told me, "We try to ignore price action as much as we can". I can't even comprehend such a backwards mentality. So why would I bother arguing with someone like that about Fibonacci? There are some fundamental extremists who are just on a completely different planet. That's fine. They can stay there. In fact, I prefer it.

Media-wise, they hate it. On two separate occasions, on two different TV networks, I've been told my the producer a couple of minutes before going on live that, "We don't use words like Fibonacci around here, so please do not mention that". I kid you not. But most of the financial media is completely lost anyway, and they're objectives are not to make money in the market, so it should not be surprising. The media is trying to sell ads and increase page views, so many of them believe that Fibonacci analysis scares their audience. Fine. Better for us.

Moving on to more important things, let's start at the beginning with how the Fibonacci Sequence was first discovered. Liber Abacci, first published in the year 1202, was a book on arithmetic written by Leonardo of Pisa. We know him today as Leonardo Fibonacci. In the book, a problem is posed that first gave rise to this sequence of numbers: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, and so on to infinity. The problem was this:

How many pairs of rabbits placed in an enclosed area can be produced in a single year from one pair of rabbits if each pair gives birth to a new pair each month starting with the second month.

From Elliott Wave Principle:

In arriving at the solution, we find that each pair, including the first pair, needs a month’s time to mature. But one in production, begets a new pair each month. The number of pairs is the same at the beginning of each of the first two months, so the sequence is 1, 1. This first pair finally doubles its number during the second month, so that there are two pairs at the beginning of the third month. Of these, the older pair begets a third pair the following month so that at the beginning of the fourth month, the sequence expands 1,1,2,3. Of these three, the two older pairs reproduce, but not the youngest pair, so the number of rabbit pairs expands to five. The next month, three pairs reproduce so the sequence expands to five. The next month, three pairs reproduce so the sequence expands to 1,1,2,3,5,8 and so forth.

So basically the sum of any two adjacent numbers in the sequence forms the next higher number in the sequence: 1 plus 1 equals 2, 1 plus 2 equals 3, 2 plus 3 equals 5, 3 plus 5 equals 8, and so on to infinity.

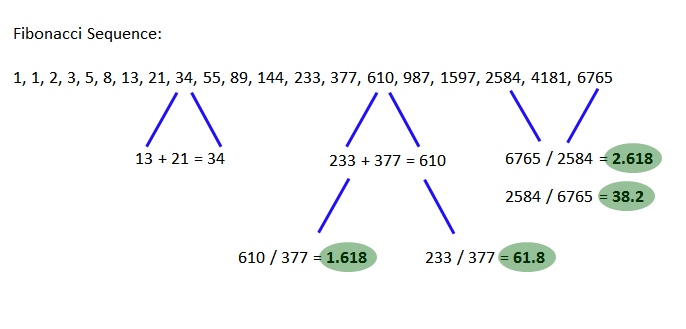
Why is this important? Well after the first several numbers in the sequence, the ratio of any number to the next one higher is approximately .618 to 1 and to the next lower number approximately 1.618 to 1. The further along the sequence, the closer the ratio approaches 0.618 (or 61.8%). Between alternate numbers in the sequence, the ratio is approximately .382, whose inverse is 2.618.

The Golden ratio is 1.618%. Here is a visual that I put together to help show how these important numbers are calculated:

These numbers circled in green are the ones we want to keep in mind as far as the market is concerned, especially 61.8% and 1.618%. There are two simple ways that these Fibonacci numbers can be used:

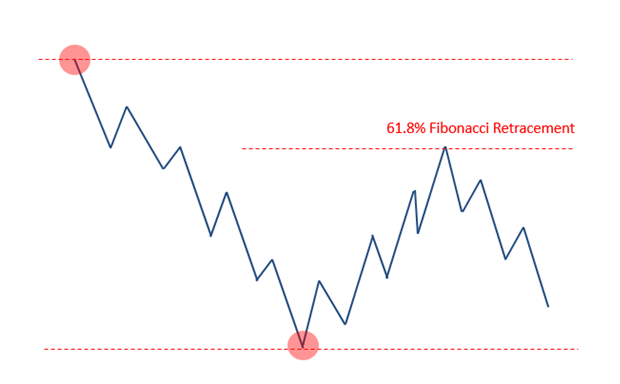
1. Retracements: Looking for the end of a counter-trend market move. In other words, to find the end of a sell-off within a larger uptrend, or to find the end of a rally within a larger downtrend. Here is an example of the 61.8% retracement coming into play within an ongoing downtrend:
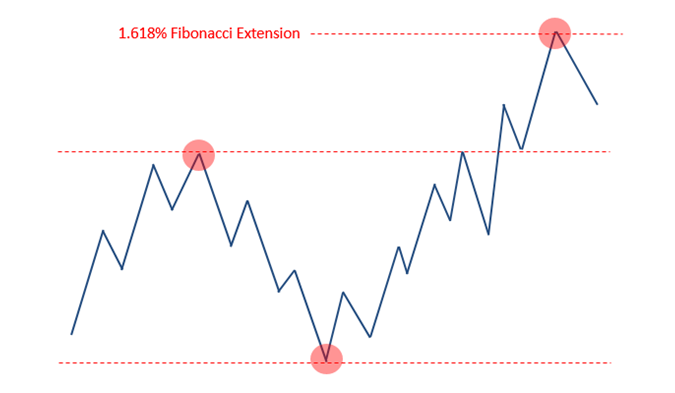
2. Extensions: Looking for targets within an ongoing market move. In other words, to find an upside target within an ongoing uptrend after taking out a previous high, or to find a downside target within an ongoing downtrend after taking out a previous low. Here is an example of the 161.8% extension coming play within an ongoing uptrend:

These Fibonacci levels can be used to calculate targets regardless of the asset class. We can be looking at U.S. stocks or sector ETFs, Indexes like the S&P500, Futures markets, Currencies, etc etc. Also, remember that the market is fractal. These levels often come into play on longer-term weekly timeframes, intermediate-term daily timeframes, and often intraday. So it doesn't matter how long your time horizon might be or what sort of vehicles you have in your portfolio, these principles can be applied across the board.

First let's talk about Retracements. When markets are in an uptrend, for example, at some point price will correct. Nothing goes straight up right? It's a stair step. Corrections within uptrends tend to stop selling off near the 38.2% retracement of the prior move or the 61.8% retracement of the prior move. If the market starts to rally again near the 38.2%, it suggests that this is a stronger uptrend compared with those who fall all the way down to the 61.8% retracement level before the rally resumes. Both are perfectly normal.

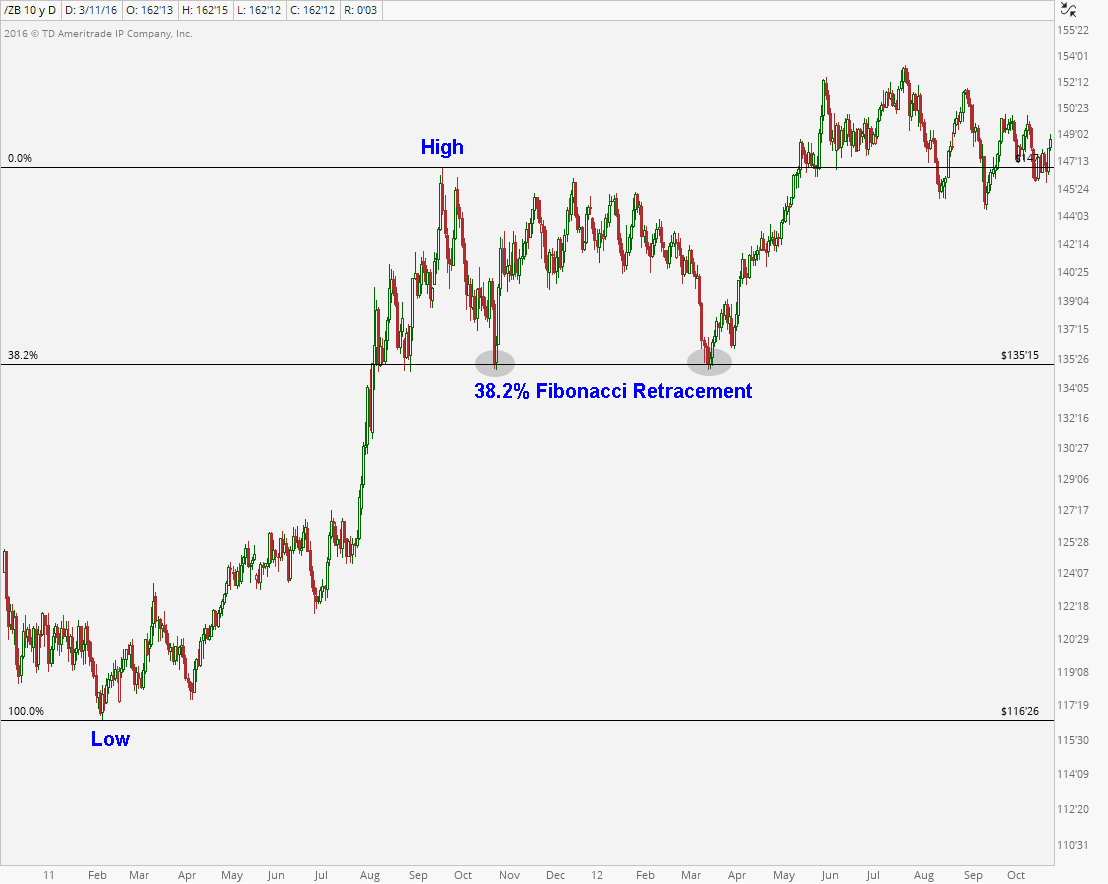
Here is an example of 30-year U.S. Treasury Bond Futures during 2011-2012. After putting in a low in February 2011, prices rallied in a nice uptrend into the Fall of that year. The correction from those highs ended by finding support near the 38.2% retracement of that prior rally. Support came into play and the rally resumed into the following year:

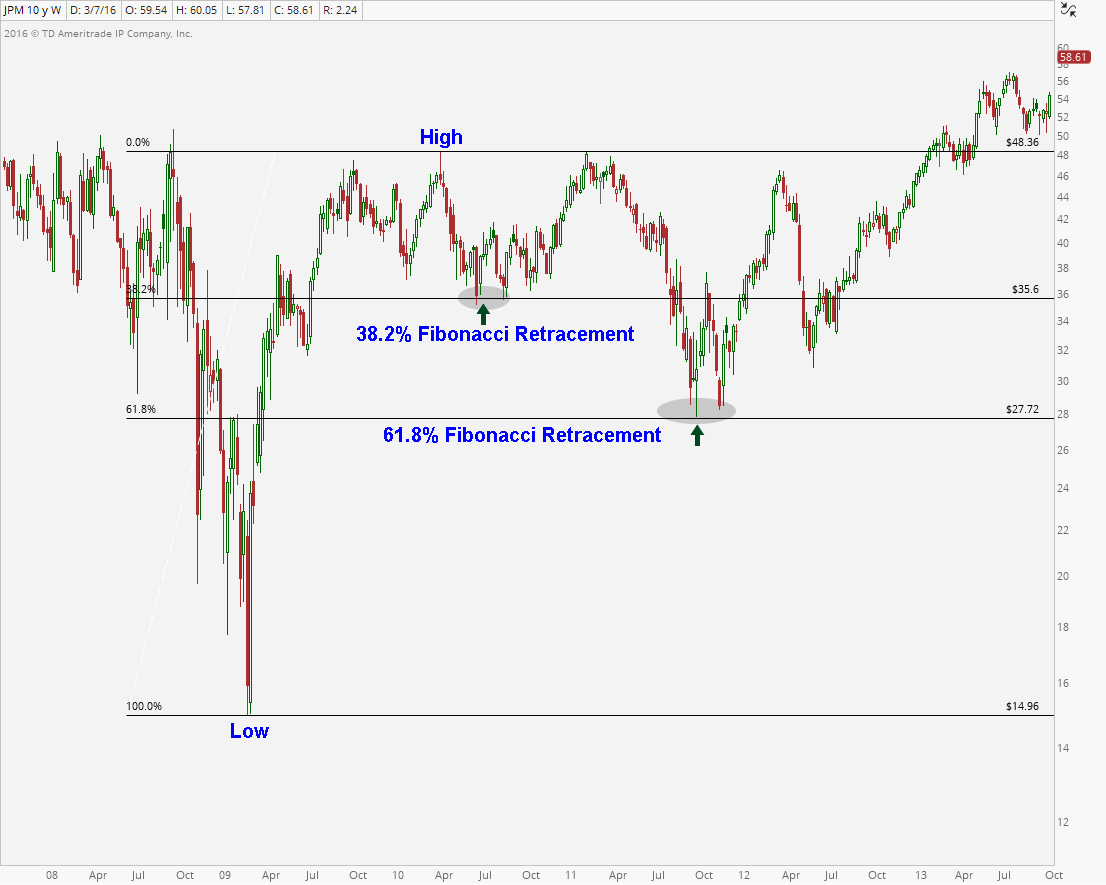
The next chart is JP Morgan $JPM back in 2009-2011. The stock put in its epic bottom in March of 2009 along with many others at the time, and then went on to rally into the Spring of 2010. The initial correction into the Summer found support right near the 38.2% retracement of that prior move. The market then went on to rally back to those former highs. After running into prior resistance, $JPM fell apart once again sending shares much lower, this time taking out those former lows near the 38.2% retracement. The next logical area of support was the 61.8% retracement of that move off the March 2009 lows. That's where the market found support and prices of $JPM went on to rally to new highs from there:

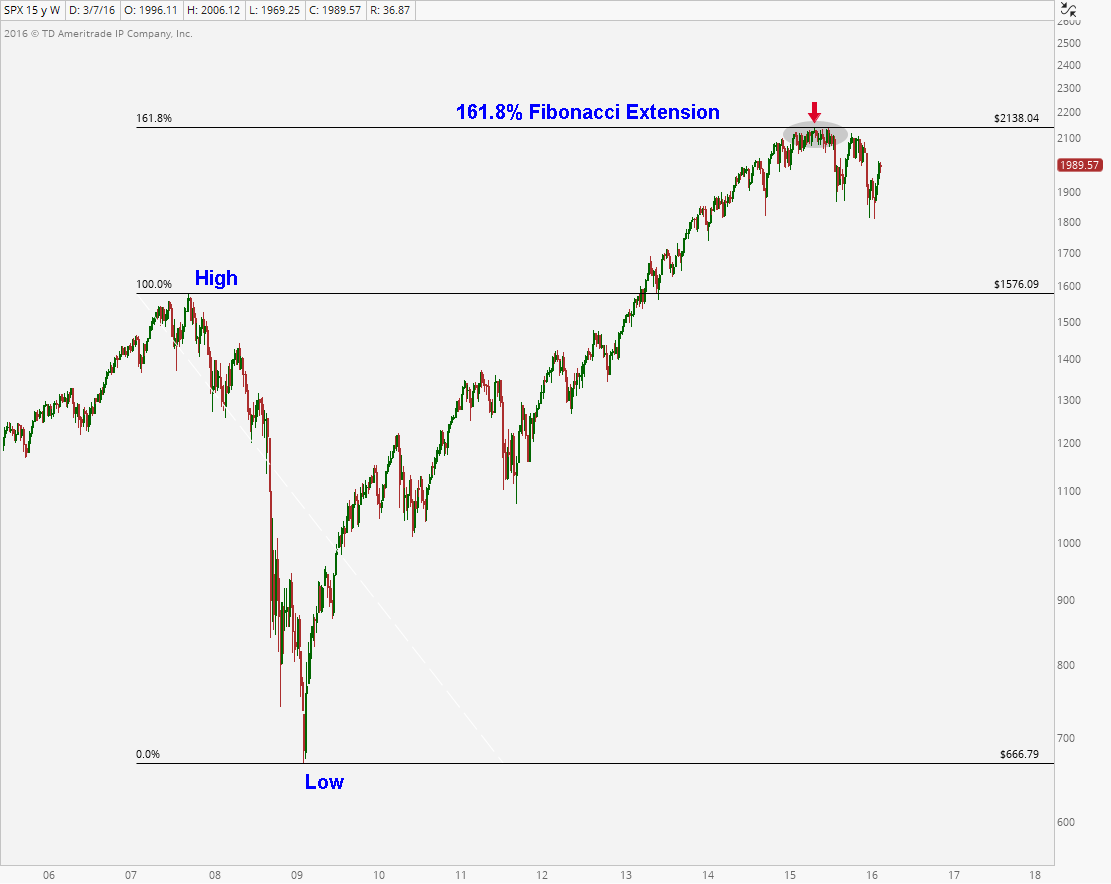
I can give you thousands of examples like these, but I think you get the idea. Next I want to talk about extensions. These are particularly useful when we are making all-time highs or all-time lows. In other words, when there aren't any former support and resistance levels to target, Fibonacci levels are very helpful. This was recently the case when the S&P500 was hitting all-time highs, uncharted territory, if you will.

Here we are looking at the S&P500 Index correcting from the 2007 highs down to the March 2009 lows. After surpassing those former 2007 highs, there weren't any support or resistance levels to trade against, so Fibonacci was where we turned. Sure enough, prices in May of 2015 stopped rallying at exactly the 161.8% extension of the entire 2007-2009 decline:

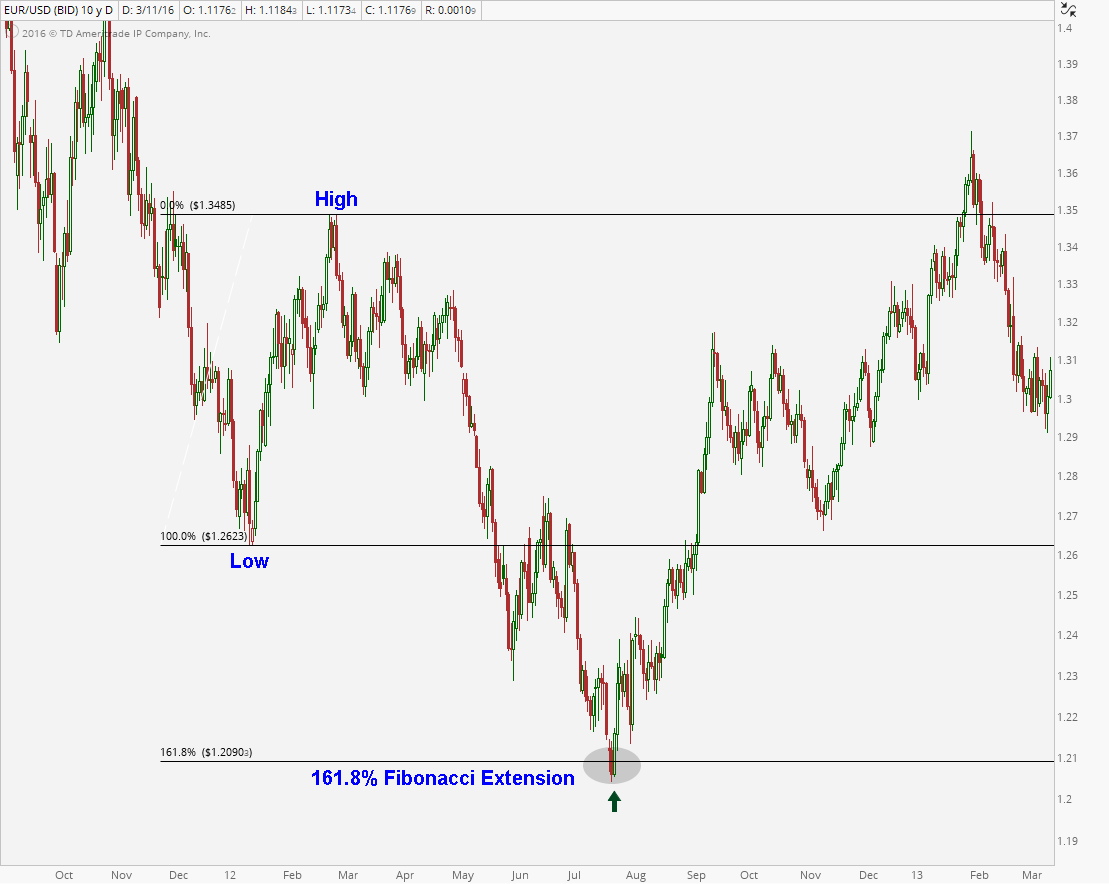
The same can be seen to the downside during downtrends. Here we are looking at the Euro vs the U.S. Dollar $EURUSD in 2012. This market put in its low in early 2012 and went on to rally for a couple of months. All of this was within an ongoing downtrend. Once prices in May took out those former lows near 1.26, the next logical target was the 161.8% extension of the prior rally. This gave us a target just under 1.21 which is precisely where $EURUSD found its bottom that Summer and then went on to rally and make new highs:

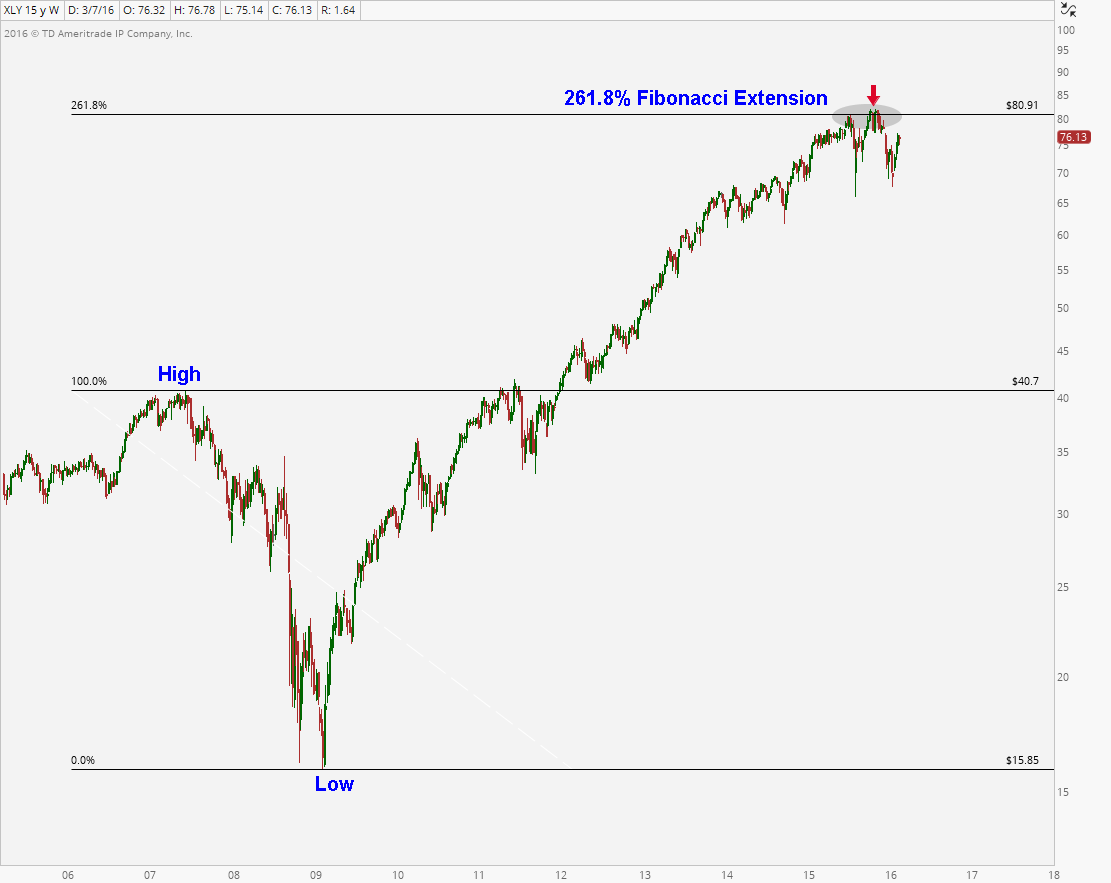
Here is a good example of a very strong market that just kept rallying relentlessly. We are looking at one of the leadership groups off the 2009 lows: Consumer Discretionaries $XLY.  You can see the high in 2007 and low in 2009, very similar to the S&P500 and other markets. As prices of this sector ETF reached the 261.8% extension of that 2007-2009 correction, the exhaustion became evident. This sector did nothing but go down since reaching that price objective:

I can go on and on giving you example after example, but I'm just going to leave it here. If you're not already a member, I highly recommend starting a 30-Day Risk Free Trial with Allstarcharts.com so you can see this Fibonacci analysis across asset classes and timeframes in real time. The Chartbook has over 300 charts, constantly updated with all of the Fibonacci extensions and retracements whenever appropriate to current trends.

One thing I would like to reiterate is that only price pays. Supply and demand is based on support and resistance defined by prior levels where shares changed hands. Fibonacci, just like every tool outside of price, is only supplemental. Fibonacci works best when either multiple Fibonacci levels cluster together, or when Fibonacci levels coincide with former support or resistance. But again, all of this is just a supplement to price, just like volume, or momentum, or the use of smoothing mechanisms, or sentiment or seasonal studies. Only price pays, but Fibonacci certainly helps.

Join Allstarcharts as a Premium Member today!

Tags: $STUDY $SPX $JPM $ZB_F $EURUSD $XLY